Projects
Offline Robot Learning
Offline Robot Validation
Marginalized Importance Sampling for Off-Environment Policy Evaluation
Reinforcement Learning (RL) methods are typically sample-inefficient, making it challenging to train and deploy RL-policies in real world robots. Even a robust policy trained in simulation, requires a real-world deployment to assess their performance. This paper proposes a new approach to evaluate the real-world performance of agent policies without deploying them in the real world. The proposed approach incorporates a simulator along with real-world offline data to evaluate the performance of any policy using the framework of Marginalized Importance Sampling (MIS). Existing MIS methods face two challenges: (1) large density ratios that deviate from a reasonable range and (2) indirect supervision, where the ratio needs to be inferred indirectly, thus exacerbating estimation error. Our approach addresses these challenges by introducing the target policy’s occupancy in the simulator as an intermediate variable and learning the density ratio as the product of two terms that can be learned separately. The first term is learned with direct supervision and the second term has a small magnitude, thus making it easier to run. We analyze the sample complexity as well as error propagation of our two step-procedure. Furthermore, we empirically evaluate our approach on Sim2Sim environments such as Cartpole, Reacher and Half-Cheetah. Our results show that our method generalizes well across a variety of Sim2Sim gap, target policies and offline data collection policies. We also demonstrate the performance of our algorithm on a Sim2Real task of validating the performance of a 7 DOF robotic arm using offline data along with a gazebo based arm simulator.
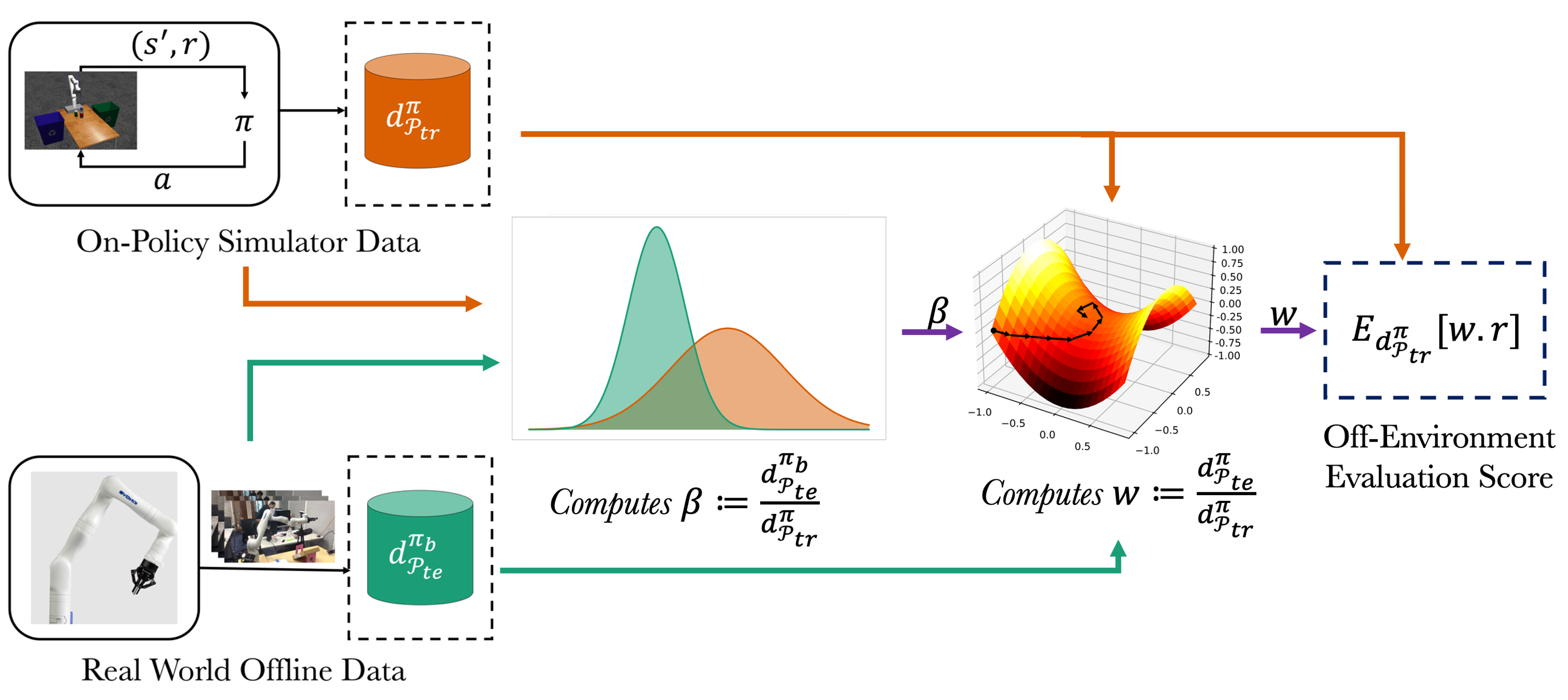
Off Envrionment Evaluation using Convex Risk Minimization
Applying reinforcement learning (RL) methods on robots typically involves training a policy in simulation and deploying it on a robot in the real world. Because of the model mismatch between the real world and the simulator, RL agents deployed in this manner tend to perform suboptimally. To tackle this problem, researchers have developed robust policy learning algorithms that rely on synthetic noise disturbances. However, such methods do not guarantee performance in the target environment. We propose a convex risk minimization algorithm to estimate the model mismatch between the simulator and the target domain using trajectory data from both environments. We show that this estimator can be used along with the simulator to evaluate performance of an RL agents in the target domain, effectively bridging the gap between these two environments. We also show that the convergence rate of our estimator to be of the order of $n^−1/4$ , where n is the number of training samples. In simulation, we demonstrate how our method effectively approximates and evaluates performance on Gridworld, Cartpole, and Reacher environments on a range of policies. We also show that the our method is able to estimate performance of a 7 DOF robotic arm using the simulator and remotely collected data from the robot in the real world.

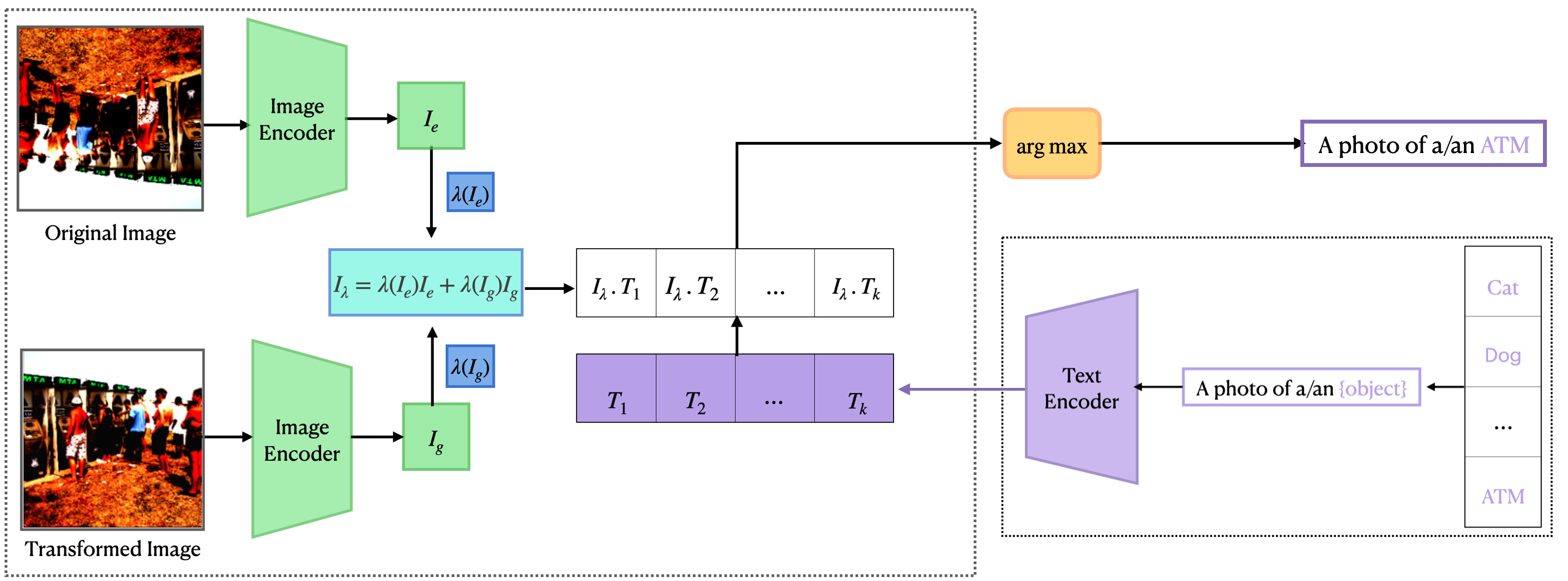
Equivariant Few-Shot Learning from Pretrained Models
Efficient transfer learning algorithms are key to the success of foundation models on diverse downstream tasks even with limited data. Recent works of \cite{basu2022equi} and \cite{kaba2022equivariance} propose group averaging (\textit{equitune}) and optimization-based methods, respectively, over features from group-transformed inputs to obtain equivariant outputs from non-equivariant neural networks. While \cite{kaba2022equivariance} are only concerned with training from scratch, we find that equitune performs poorly on equivariant zero-shot tasks despite good finetuning results. We hypothesize that this is because pretrained models provide better quality features for certain transformations than others and simply averaging them is deleterious. Hence, we propose λ-\textit{equitune} that averages the features using \textit{importance weights}, λs. These weights are learned directly from the data using a small neural network, leading to excellent zero-shot and finetuned results that outperform equitune. Further, we prove that λ-equitune is equivariant and a universal approximator of equivariant functions. Additionally, we show that the method of \cite{kaba2022equivariance} used with appropriate loss functions, which we call \textit{equizero}, also gives excellent zero-shot and finetuned performance. Both equitune and equizero are special cases of λ-equitune. To show the simplicity and generality of our method, we validate on a wide range of diverse applications and models such as 1. image classification using CLIP, 2. deep Q-learning, 3. fairness in natural language generation (NLG), 4. compositional generalization in languages, and 5. image classification using pretrained CNNs such as Resnet and Alexnet.
Towards Provable Log Density Policy Gradient (On-going)
Policy gradient methods are a vital ingredient behind the success of modern reinforcement learning. Although modern policy gradient methods have achieved state-of-the-art performance over a variety of complex tasks, their practical implementation introduces a residual error term in gradient estimation. In this work, we argue that this residual term is significant and that correcting it will lead to a sample-efficient reinforcement learning. We also propose a new method called log density gradient to estimate the policy gradient, which corrects for this residual error term. Our method computes the policy gradient as the gradient of the log of the average state-action discounted distribution multiplied by the reward function. We first present a method to exactly calculate the log density gradient for a tabular Markov Decision Processes (MDPs). Further, we show that such a method for estimating policy gradient always gives us a unique solution irrespective of the discounting factor. For more complex environments, we propose a temporal difference (TD) method that approximates log density gradient using on-policy samples. We show that this TD method is a contraction and converges to the optimal solution under linear function approximation. We then propose a min-max form that can approximate the log density gradient over other non-linear function classes such as neural networks. Finally we show that the sample complexity of our min-max form to be of the order of $n^{-1/2}$, where $n$ is the number of on-policy samples. This sample complexity bound is significantly better than the sample complexity of vanilla policy gradient methods, indicating a promising novel direction to develop reinforcement learning algorithms that require fewer samples.
